HOME

Kayaks Designs comparison page

  Perhaps the easiest way to size a kayak is to have a visual frame of reference such as other kayak designs. This page brings all One Ocean Kayaks together, side by side, for relative comparison of scale as well as the technical stuff such as wave and viscous resistance.
 Kayak scale table
The kayak profiles below show the exact scale and proportion of the designs relative to each other.
Resize your browser to full screen for better viewing. Click on images for kayak technical specs (particulars).
 
  Cape Ann Double

  Cape Ann Expedition

  Cape Ann HV - scaled from Cape Ann

  Cape Ann

  Storm

 Cirrus and Cirrus Hybrid

  Expedition Sport - scaled from Expedition

  Storm LT - scaled from Storm

  Cirrus LT and Cirrus LT Hybrid - scaled from Cirrus
 
  Storm SLT - scaled from Storm

  Cirrus SLT - scaled from Cirrus
 
top
 
.
 Wave resistance and friction drag charts
The charts below represent the theoretical performance potential of One Ocean Kayaks hullforms. The input of all the variables into the 'drag prediction algorithm' allows quite a bit of flexibility and interpretation. Therefore, the results should be taken less for their absolute value than as an insight into the kayaks performance relative to each other. Comparisons to other kayak designs can be considered absolute only if the same criteria were applied in all instances. The analogy of two cooks preparing a meal from an identical recipe and both dishes come out tasting totally different is very apt in a case like this.
Resize your browser to full screen for better viewing

 NOTE: Some of the graphs are too close together for visual comparison. The table of numbers below the chart indicates the 'y axis' values for each kayak.
.top

Frictional Resistance (viscous drag)

Since viscous resistance in the graph is plotted against speed the most significant difference among the kayaks is their wetted surface. It is therefore not surprising that the viscous drag will be the smallest for the smallest kayak (Storm SLT) and progressively larger with each larger kayak design.

As the hull plows through the water, a thin layer of water trapped in the 'roughness' of the surface is dragged along with the hull. Since the 'trapped' water molecules are in contact with many other molecules further from the hull, their kinetic energy is transferred progressively through 'layers' further from the kayak skin. This viscous interaction of water molecules is confined in a space called the boundary layer. The boundary layer is where water causes 99% of Frictional resistance.

When you think of kinetic energy transfer between water molecules, a game of billiard is a good analogy. A 'simple' chain reaction initiated by one ball hitting other balls that hit other balls.... This energy transfer essentially 'bleeds' the energy of the kayak into the turbulence of the surrounding water.
You may remember from school that kinetic energy is a function of mass and velocity such that:
E(kinetic)=0.5 x m x V^2
It is not surprising that theoretical frictional resistance also varies with the square of speed. In the real world it is a bit less since frictional resistance further subdivides into laminar flow resistance and fully turbulent flow resistance. Despite the difference, the formula below lumps them both together.

Viscous drag (Rf) depends on the following:

  • wetted surface area - S (m^2)
  • speed of the hull - V (m/s)
  • viscosity (mu)
  • kinematic viscosity (nu)
  • density of water (rho)
  • coefficient of friction- Cf (assumes smooth hull) no units
  • length of waterline- L(m)
Rf = 0.5 x (rho) x V^2 x S x Cf
in units -> kg/m^3 x (m/s)^2 x m^2 = kg x m/s^2 = mass x acceleration = force

Cf = 0.075/(log (R)-2)^2
R (Reynolds number) = (V x L)/(nu)
(nu)kinematic viscosity = (mu)/(rho)
(nu) is a constant for water salinity and temperature
. top

Wave Resistance (residual resistance)


Explanations of the coefficients are on the Hydrostatics page.

Unlike viscous drag, wave resistance is far more complicated to calculate for it takes into account many more hull parameters as well as other factors which are beyond the scope of this page (at this point).
Note from the graph that wave resistance doesn't really play much role in recreational paddling speeds under 4 knots but the difference between the hull forms becomes much more prominent at higher cruising speeds (4-5 knots).
As the longest hull in the group, the Double will predictably have the smallest wave resistance. The Expedition shows the lowest wave resistance at speeds of 3.5 - 5 knots which covers almost the entire envelope of 'normal' paddling. The Storm comes close second after the Expedition, but supersedes it at speeds over 5 knots.
Most recreational paddling speeds are about 2 - 3.5 knots. Energetic cruising speeds are largely in the 3.5 - 5.5 knots range. Speeds higher than 6 knots are in the realm of long distance racing and sprinting. Olympic sprint speeds average 9.98 knots (off the chart ).

Wave drag depends largely on the following:

  • displacement
  • speed of the hull
  • BWL - waterline beam
  • draft
  • LWL - waterline length
  • EWL - effective waterline length
  • LCB - longitudinal center of buoyancy
  • Cp - prismatic coeff.
  • Cb - block coeff.
  • Cm - midship coeff.
  • angle of entry exit
  • form factors (adjustment due to hard chines, appendages, stern and bow shape etc...)
.top

Total Resistance

Total resistance is the sum of frictional and wave resistance. (If you added the Frictional resistance graph to the residual drag graph you would get the chart on the left)

The blue line for the double shows the largest resistance but remember there are two people to share the load, so if you divided the total resistance, each paddler would need to exert less energy than in any of the single kayaks.
Take for example the total double resistance at 4 knots. It is 4.53lb and if you divide it in two, each paddler has to exert only 2.26lb. The Cape Ann Double will easily beat the pants off any single kayak even if one of the double's partners doesn't do their fair share of the work :)

The StormSLT has the lowest total resistance across the entire speed range making it the ideal cruising kayak for lighter paddlers with less physical strength.

.top

Coefficient of total resistance vs. volumetric Froude number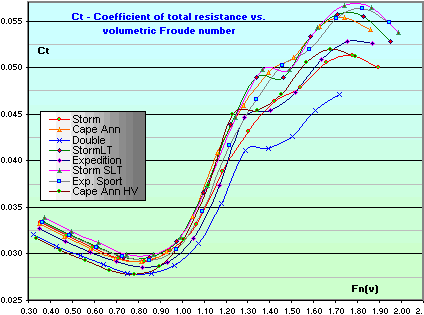



The lower the graph at each point, the more efficient the kayak. The blue line of the Double has practically the highest efficiency across the entire speed range with the Expedition following second but the Cape Ann HV is by far the most efficient kayak up to the Fn = 0.8 and second best up to the 0.9 mark which corresponds to a cruising speed of about 4 knots. This is not surprising since its wetted surface relative to the volume below the waterline (the Area/ Dispacement ratio) is currently the lowest of all the kayaks. Consequently, the HV as well as the Double and Expedition perform very well at moderate speeds with generous loading. The Storm is very close to the Cape Ann at lower speeds but becomes far more efficient at higher speeds beyond the Fn = 0.9 mark.
The Expedition Sport shows the second lowest Total resistance between 3.5 - 5.5 knots. It also ranks as a relatively efficient kayak (after the Expedition and the Double) between Fn 0.85 and 1.05 (3.5 to 4+ knots)

Total drag vs. Efficiency distinction
It is quite clear from this chart that kayaks with longer waterline and larger displacement (or any boat for that matter) will generally be more efficient, that is, they will experience less drag with respect to the amount of 'stuff' they can carry. Take for example a long ship carrying many tons of cargo. The drag on such ship would be obviously enormous but it would still take less energy to transport all this cargo than having it transported in hundreds of same shape, kayak-sized boats. The drag on the small boats together would far exceed the total resistance of the large ship, thus the large ship would be more efficient. This is a very extreme example, but it illustrates the concept more clearly than cases in which subtle differences do not provide much insight into the principles at play.

This chart really shows the relative efficiency of the hulls adjusted for displacement (that is why the volumetric Froude number as the horizontal x-axis).
The interpretation is different (than with speed) and may be a little confusing because the volumetric Froude number takes into consideration BOTH speed AND volume at the same time.

Fn= V / (g^-1/2 x D^-1/6) (nondimensional)

V - speed (m/s)
g - gravitational acceleration (m/s^2)
D - displacement (m^3)
It may be mysterious that the equation is formulated as it is but if you substitute units in the Fn, everything will conveniently cancel out - that is why. You may have seen another Froude number which takes into account speed and waterline length as in:

Fn= V/(gL)^1/2

L - length of waterline (m)
If you substitute the units, everything will cancel out here as well. This Froude number is essentially the "speed / length" ratio so often talked about in relation to prismatic coefficient, 'hull speed' and wave resistance.

Finally, here is the definition of the Ct (coefficient of total resistance)

Ct = Rt/(1/2 x (rho) x V^2 x D^2/3)

Rt - are the values in chart #3
Again the divisor term units work out to become the units of force (kg x m/s^2) so that the entire coefficient becomes nondimensional.

top  
         
Back to Kayak Designs | Plans | Kayaks in Plans

Home Kayak Designs Kayak Shop Materials Kayak Gallery About us
Building Manual Plans Sandwich Core Wood Kayak Order E-mail
Epoxy Test Abrasion Cloth Rudder Resources Choosing Kayak Guestbook

If you notice any problems with the site (i.e. error links, missing images) please, let me know. Thanks

Mail:
Vaclav Stejskal
10 Colonial Court apt. 73
Stoneham, MA. 02180
           USA
Tel:  781-481-9261

E-mail  

© 1999 - 2020 Copyright Vaclav Stejskal
All rights reserved
Last page update: 11 January 2020